A TR 1.0 bemutatása | Modell összehasonlítás | TR 1.0 elmélete
| Regionális szabályozás modellje | Országos szcenárió analízis

Proceedings of the Fourth International Clean Air Congress,
Tokyo, Japan 1978, 284-287

Szepesi D. J.:

Modified roll-back model for air quality planning


Summary of major findings

For the quantitative analysis and forecasting of the quality of ambient air proper tools are necessary. Such tools are meteorological simulation models. In this paper an advanced version of a simple roll-back model reported by Moris and Slater (1974) is presented.

This model is based on the following principle of proportionality: The quality of air to be attained in the n-th year in an emission control area is proportional to the air quality measured in the initial year as well as the quality of air calculated for the n-th year is proportional to the air quality calculated for the initial year. The above principle of proportionality is expressed by the following algorythm:

[khi(yn)-khi(b)]goal / [khi(0ym)-khi(b)]meas. =

sum (i=1...4) {[khi/Q]ni * Q(ni)}calc. / sum (i=1...4) {[khi/Q]0i * Q(0i)}calc.,

where

khi(yn) [microgram/cubic m] - the yearly air quality norm value,
khi(b) [microgram/cubic m] - value of background concentration,
khi(0ym) [microgram/cubic m] - yearly mean value of air quality measured
in the emission control area,
index i of the source category is: 1 ground level source, 2 area source,
3 point source, 4 tall stack,
Q(ni) and Q(0i) [t/year] - emission of the i-th source category
in the n-th and the initial year, respectively,
[khi/Q]ni and [khi/Q]0i [microgram/cubic m/t/year] - relative concentration value of
the i-th source category
in the n-th and the initial year, respectively.

Relative concentration

for ground level:
 [khi/Q] (n=0, i=1) = [C1(Z-1.5)M] / [D(uz+0.5)Z x]
for area source:
 [khi/Q] (n=0, i=2) = C2 M / uz T
for point source:
 [khi/Q] (n=0, i=3) = C3 M / [pi e uh sigma(y).sigma(z) N]
for tall stack:
 [khi/Q] (n=0, i=4) = C4 M / [pi e uh sigma(y).sigma(z) N]

where

C1=7, C2 =30.72 empirical constants,
C3=0.002, C4=0.0006 conversion factors of the one hour maximum concentration value into yearly average for the whole control area,
M=31700 conversion factor,
Z [m] average height of buildings,
D [m] average width of the main road,
uz, uh [m/s] mean wind speed value at the roof top and at the average height of the chimneys,
x [m] length of the main roads in the control area,
T [square m] area of the emission control region,
N number of industrial establishments having point sources in the control area,
sigma(y).sigma(z) [square m] product of the horizontal and vertical crosswind components of atmospheric dispersion for normal stratification of the atmosphere, which can be determined by the aid of Figure 1b,
h [m] average height of the chimneys in the emission control area.


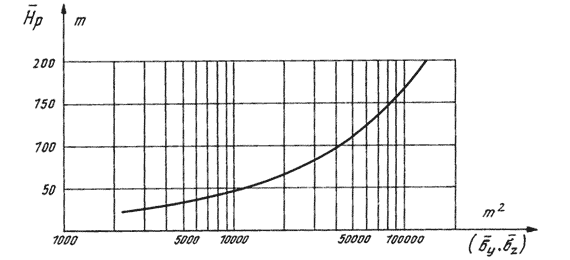
Figure 1b.
Product of sigma(y) and sigma(z) against the height of the source

The model presented gives a good approximation if the following conditions fulfilled:

a) The measured air quality data are characteristic for emission control area.
b) The value of background concentration remains unchanged.
c) The diffusion climatological factors will not change during the period investigated.

The model presented takes into account the simultaneous polluting effects of different source categories. According to example shown here, the most intensive pollution is due to ground level sources as well as area sources. A much less effect is caused to the ambient air by point sources and tall stacks. The comparison of the relative concentration values for the 4 source categories gives the following ratios of the polluting effectiveness:

Ground level s. : Area s. : Point s. : Tall s. = 500 : 300 : 3 : 1.

References

Morris, R. et al., Modified Rollback Models. Proc. 5th Expert Meeting on Air Pollution Modelling. Comitteee on the Challenges to Modern Society, Denmark (1974).