|
A
TRANSZMISSZIÓ 1.1 ELMÉLETE
Euroconform
Regulatory Transmission Modeling for Hungary, Part 1
Dezső J. Szepesi
Katalin E. Fekete
CARM Inc., H-1137
Budapest, Katona J. u. 41. V/25, Hungary
Richárd Büki
MS of HDF, H-1885, P. O. B. 25, Budapest, Hungary, E-mail: rbuki@hotmail.com
Abstract - In
Part 1 this paper describes the theoretical and practical steps
(correct mathematical and atmospheric-physical simulation, temporal
and spatial representativity of input data, scrutinized QA/QC, testing
and validation during programming) carried out to achieve a new
euroconform regulatory model called TRANSMISSION 1.1 for Hungary.
Simultaneously in another development planetary boundary layer modeling
has been prepared including input data standardization and processing
for the whole country used by US EPA type AERMOD model family. Description
of these efforts will be published in Part 2 in this periodical
soon.
Key-words: Actual
sector average concentration, centerline concentration, meteorological
data base, modeling, most frequent meteorological situations, most
probable concentration, norm exceedency, regional scale wind field,
regulatory modeling, Szepesi-type stability categories, temporal
and spatial representativity of meteorological data, temporal transmission
data series, transmission, transmission matrix.
1. Introduction
Recently new
euroconform air quality laws ([1], [2], [3] and [4]) were promulgated
and adopted for Hungary. To meet the requirements of these laws,
the set up of a new regulatory model system named TRANSMISSION 1.1
(in EEA Model Catalogue HNS-TRASMISSION : .http://pandora.meng.auth.gr/mds/strquery.php?wholedb&MTG_Session=bd2abde34287fec71d8de94715c997fc
) was necessary.
By doing this following principles were honoured:
- Correct
mathematical and atmospheric physical simulation,
- Scrutinized
application of QA/QC procedures during the whole modeling project,
- Built-in
meteorological database (transmission matrices, time-series, most
frequent meteorological situations) for the whole country,
- Application
of temporally and spatially representative meteorological databases,
- Availability
of the same standardized transmission model system for users and
inspectors ensuring the principle "same input - same output".
2. Concepts
and definitions
The first works
describing this topic were published in Hungary in 1967, 1970 and
1985.
This article is to present recent developments achieved in this
field. We introduce among others a new notion, called average concentration
for the actual sector, which is similar to the most probable concentration,
but refer to a narrower sector. The difference is in the definition
of the borders of the sector. In the new definition we use the concept
of Meade and Pasquill [6], this means that the border of the sector
is at the line of the 10 per cent value of the ground-level centerline
concentration.
It will be shown that this newly introduced notion can be simply
estimated by multiplication of the ground-level centerline concentration
by a constant. Finally we introduce a new factor which is vital
in estimating the norm exceedencies of the 1 hour maximum concentration.
Let us see the basic definition we should use, introducing the concept
of the average concentration for the actual sector. The concentration
is assumed to have Gaussian distribution.
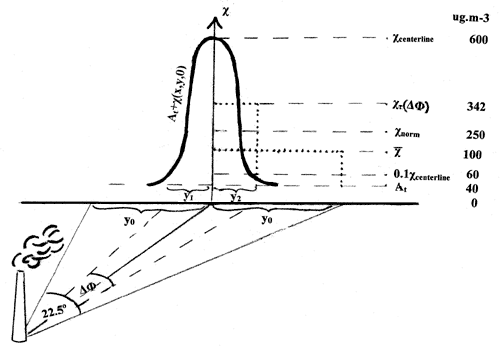
Figure 1.
The Gaussian distribution and estimation of the different
types of concentration
2.1 Estimation
of ground-level concentration from an elevated point source
This well-known
Gaussian formula specifies the concentration at the ground along
the downwind distance of x from a point source:
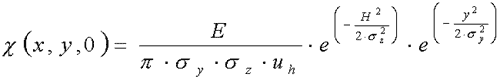 (1) (1)
Where:
X(x,y,0):ground level concentration, µg•m-3
x: the downwind distance from the source, m
y: crosswind distance, m
z: height above the ground, m
E: emission, µg•s-1
pi: constant, 3.1415
sigma y: crosswind dispersion, m
sigma z: vertical dispersion, m
uh: wind speed at source-height, m•s-1
H: effective height of the stack, m.
2.2 Estimation
of the ground-level centerline concentration from an elevated point
source
This is a special
case of Eq. (1) when y=0.
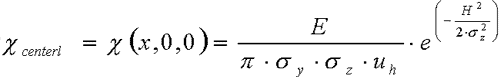 (2) (2)
This type of
maximum concentration occurs rarely, but according to the new air
quality laws ([1], [2], [3], [4]) this has to be taken into account
for determining the range of significant impact for EIA's.
The similar
denotations are valid as before.
2.3 Estimation
of the most probable concentration
This definition
is also introduced by [5]:
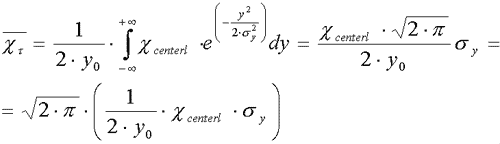 (3) (3)
Where:
khi tau: most probable concentration, µg•m-3
y0: crosswind length belonging to meteorological wind sector (22.5o),
m
khi centerl: the ground-level centerline concentration, as defined
in (2), µg•m-3
The other expressions used are the same, as before.
This type of
formula is used in the model for estimation of mean and maximum
24 h and yearly mean ground level concentration.
2.4.
Estimation of the average concentration for the actual sector
Based on a suggestion
of Meade and Pasquill [6], we define this type of concentration
distribution. The concentration is the integral between the 10 percent
limits of the ground-level concentration.
In the first step we calculate the limits of the integral, which
was in the previous case ±?. Because of symmetry case, y1=y2, the
basic equations are:
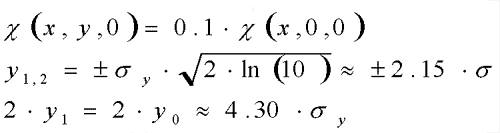 (4) (4)
Where:
y1, y2: crosswind distances belonging limits of sector delta phi,
m
Resulting from
this transformation, we have got the average concentration for the
actual sector (delta pi). With help of the Taylor-series and the
definition of the exponential function:
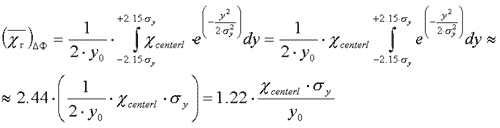 (5) (5)
Comparing
Eq. (3) to the Eq. (5) we can see that the difference between the
concentrations calculated between ±? and between the borders suggested
by Meade and Pasquill is negligible, only about 2.7%.
Substituting y0 from Eq. (4) and Eq. (5) we have got:
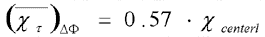 (6) (6)
The
multiplication factor 0.57 is a constant, because the crosswind
dispersion sigma y effects both khi centerl and y0 similarly, so
at the simplification it falls out.
This is the critical formula used by Hungarian environmental inspectors
to qualify whether a source complies with norms and the allowable
norm exceedencies or not.
3. Practical considerations
The correct
estimation of norm exceedencies is vital for air resources management,
air quality controll and air quality planning. If we calculate the
1-hour concentration plus the base-pollution, we should divide this
sum by a factor denoted by 'e'. So the yearly number of cases,(Nt(w,x)),
when concentration is above the limit value is the function of wind
direction,w, downwind distance,x, wind speed,u, and atmospheric
stability, S, beside of the source parameters:
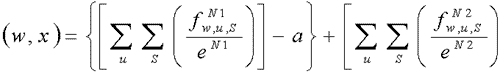 (7) (7)
Where
- fN1w,u,S : is the number of cases when the sum of the ground-level
concentration and basic pollution is over the 1 hour norm with a
tolerable degree,
- fN2w,u,S: is the number of cases when the sum of the ground-level
concentration and basic pollution exceeds the 1 hour norm more,
than tolerable,
- a: the number of cases with allowable exceedencies,
- eN1, eN2: factors of normalization to divide the number of cases
fN1w,u,S and fN2w,u,S.
Definition
of the factor "e"
Practically
the factor "e" is the ratio of the crosswind width of
the 22.5o sector and the crosswind width of the sector, where the
concentration is greater, than the limit. Starting from this principle,
the factor "e" can not be less than 1. As we can see in
Fig. 2, the value of "e" varies between 1 and 21 depending
on the meteorological and physical conditions.
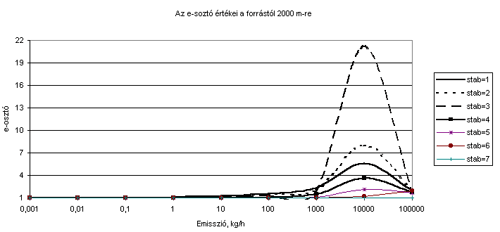
Figure 2.
The value of "e" at a distance of 2000 m from the
source Deduction of algorythm for 'e'
Considering
the geometry of Fig. 1 and the definition of the factor "e":
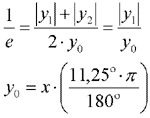 (8) (8)
The
inequality, which has to be solved, is:
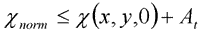 (9) (9)
After
some transformations and defining the ?At as the difference below:
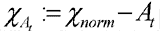
The
Eq. (9) has the form:
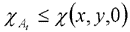
Where: khi norm:
the limit value of the concentration, µg•m-3
At: basic pollution, µg•m-3.
Let us denote a source type factor Q, as:
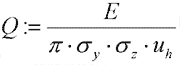 (10) (10)
We
obtain:
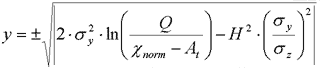
Because only
the positive resolution of Eq. (8) has physical meaning, so we obtain
the following algorithm for the factor "e":
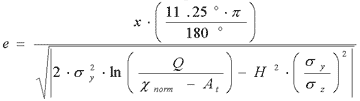
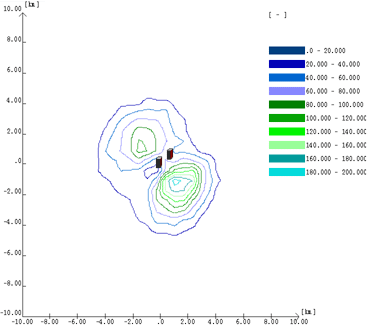
Figure 3.
Yearly number of 1 hour maximum concentration exceedencies
around point sources
An example of
the yearly number of 1 hour maximum concentration exceedencies estimated
by TRANSMISSION 1.0, the official regulatory model in Hungary is
shown by Fig. 3 for a two-source configuration with emissions of
400 kg/h and 250 kg•h-1 NO2, stack heights 70 m and 40 m, respectively,
and norm of 100 µg•m-3, basic pollution of 20 µg•m-3.
4. Regional scale diffusion climatology
The basic idea
of meteorological data preprocessing is that for ground level concentration
estimations it is more representative to use regional scale meteorology
- in other words average meteorology for an area of 20-30 km diameter
- instead of measurements made at a single point. This is called
spatial representativity or regionalization of meteorological data.
The method of data regionalization is described at [5] here we only
summarize the main steps.
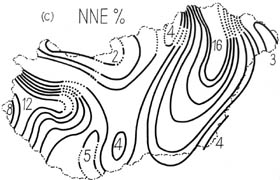
This is a non-computerized (graphical) data assimilation technique.
After plotting all wind direction and speed data available (sixteen
directions and for each direction mean speed data, respectively)
we can analyze these charts graphically, one by one (See Fig. 4
and Fig. 5). Over mountainous areas isofrequencies are denoted by
dots. These maps make possible to pick up or interpolate average
yearly wind direction frequencies and mean speed values data for
any point of the country.
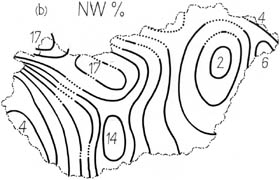 
|
Figure 4.
Relative frequencies of NW wind directions
|
Figure 5
Relative frequencies of NNE wind directions
|
The next step
is to preprocess transmission matrices based on 5 years of measurements.
This period (1958-1962) was selected because of having similar weather
characteristics as the 100-year period (1880-1980) had. In other
words the frequency distribution of macrosynoptic (Péczely) weather
types were nearly similar in both periods.
The last step is to apply K.Tar's circular polar smoothing process
[7] then using interpolation technique built in the model TRANSMISSION
1.1 to interpolate data matrices to any point of interest over the
country.
Transmission matrices gained this way and built in the model will
be temporally and spatially representative and serve as readily
applicable input data base.
Evaluation of the most frequent meteorological situations was another
important task. This was carried out by the following way. Since
atmospheric stability category S=6 (Szepesi stability 1-7 see [5])
is the most frequent one, surface wind speed prevailing during this
stability conditions were evaluated over Hungary. The numerical
values ranged from 1.6 m•s-1 to 3.1 m•s-1. These parameters are
essentials for the estimation of the range of significant impact
(RSI) (1, 2, 3 or 4). Fig.6 shows an example of RSI estimation,
for the following source parameters:
Source height
70 m and 40 m, emission 80 kg•h-1 and 50 kg•h-1, u=2,5 m•s-1, basic
pollution 20 µg•m-3, norm=100 µg•m-3, surface roughness 0.5 m.
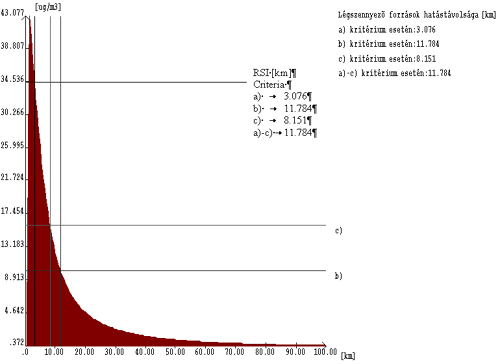
Figure 6.
RSI in km for NO2, emitted by high sources
For estimation
of 24 h mean and maximum concentrations time series of meteorological
data for 7 regions were included
5. Characteristics
of model TRANSMISSION 1.1
By using modules
detailed under points 2 and 3 a regulatory model TRANSMISSION 1.0
was prepared to satisfy the new euroconform air quality laws for
Hungary.
Major characteristics are the followings: It estimates ground level
concentration and deposition emitted by point, area and volume sources
- up to 50 -, and located at different points. It calculates 1 h,
24 h and yearly average, maximum values and norm exceedencies. Their
outputs are in table or areal distributions on EOV maps in user
selected coloured form. Dry deposition and transformation modules
are included as well.
Effects of inhomogeneous roughness, basic pollution and orographical
effects in homogeneous or inhomogeneous distributions can also be
simulated.
6. Summary
Firstly, we
reviewed definitions used in the field of air quality modeling,
and air quality planning. A new definition, 'the average concentration
for the actual sector' was introduced, which is more adequate to
the theory of Pasquill and Meade, than the definition used before.
It occurs more frequently than the centerline concentration, so
it is more realistic for air quality control purposes. Secondly
we defined and estimated the normalization factor "e",
which is the function of meteorological parameters like wind speed,
atmospheric stability, air temperature; and source data like emission
of the source, the effective stack height and the distance from
the source.
Then we detailed
some ideas and steps of carrying out meteorological data preprocessing,
the estimation of the range of significant impact and 1 hour maximum
concentrations and norm exceedencies by the official, regulatory
model TRANSMISSION 1.1 in Hungary.
Literature
[1] Magyar Közlöny
(Official Government Gazette) 14/2001. V.9. Emission and Immission
Norms. Budapest, Hungary
[2] M.K. ( O.G.G.) 20/2001. II.14. Environmental Impact Assesment.
Budapest, Hungary.
[3] M.K., (O.G.G.) 21/2001. II. 14. Clean Air Act. Budapest, Hungary.
[4] M.K., (O.G.G.) 120/2001 VI.30. Modifications. Budapest, Hungary.
[5] Fekete K., Popovics M., Szepesi D., 1983: Légszennyező anyagok
transzmissziójának meghatározása ( Guide to Estimate the Transmission
of Air Pollutants) OMSZ Hivatalos Kiadványai LV. Kötet
[6] Meade P.J. and Pasquill, F. 1958: A Study of the Average Distribution
of Pollution around Staythorpe. Int. Journal of Air Pollution, 1.
60.,
[7] Tar Károly, 1991: Magyarország szélklímájának komplex statisztikai
elemzése.(A Complex Statistical Analysis of Wind Climatology in
Hungary), OMSZ Kisebb Kiadványai67. szám
[8] Fekete K. and Szepesi D., 1983: Simulation of atmospheric acid
deposition on a regional scale. Environmental Management, Vol. 24,
pp. 17-28.
[9] Szepesi D., 1967: Légszennyező anyagok turbulens diffúziójának
meteorológiai föltételei Magyarországon (Meteorological Conditions
of the Turbulent Diffusion of Atmospheric Pollutants in Hungary)
OMI Hivatalos Kiadványai XXXII. Kötet
[10] D.J. Szepesi, K.E. Fekete and L.Gyenes: Regularory Models for
Environmental Impact Assessment in Hungary. Int. J. Environ. and
Pollution, Vol. 5, Nos 4-6, 1995.
|